CPUs are very good at doing things in parallel, even in a single core context. Indeed, speculative execution of code and instruction reordering helps the CPU ensure that the pipeline is always full. However, data dependencies in the sequence of instructions might cause the CPU to have to wait for data, be it from the L1 cache or the much slower RAM storage. Francesco Mazzoli shows in their blog post, Beating the L1 cache with value speculation , that optimizing the critical path will in some conditions yield huge performance improvements.

This article demonstrates that this optimisation can be implemented in the OCaml programming language. Knowing how OCaml values are represented in memory is useful, here is a chapter of Real World OCaml on that matter: Memory Representation of Values.

# Fast list iterations using one simple trick™

Let's start by instantiating a linked list of 10000 random numbers.

let l = List.init 10000 (fun _ -> Random.int 1024)

Now, let's sum the numbers 100k times and see how long that takes. To obtain these statistics, perf stat was used with the default settings on programs compiled with OCaml 5.0.

let rec sum (accumulator: int) (cell: int list) =
  match cell with
  | head::tail -> sum (accumulator + head) tail
  | [] -> accumulator

for _ = 1 to 100000 do
  ignore (sum 0 l)
done

 Performance counter stats for './a.out sum':

          1 368,91 msec task-clock:u                     #    0,999 CPUs utilized
     4 835 597 233      cycles:u                         #    3,532 GHz
     9 005 641 989      instructions:u                   #    1,86  insn per cycle
     3 001 229 709      branches:u                       #    2,192 G/sec
           195 819      branch-misses:u                  #    0,01% of all branches

Conveniently, we're doing one billion additions (10000 list items, repeated 100k times). So each iteration is taking:

• 1.36 nanoseconds
• 4.8 cycles
• 9 instructions
• 3 branches

We can already see that the CPU is cramming multiple instructions per cycle. Using the compiler explorer, the following assembly is obtained:

camlExample__sum_268:
        subq    $8, %rsp
.L101:
        cmpq    (%r14), %r15         # check if GC is waiting for us
        jbe     .L102                # branch #1
.L103:
        testb   $1, %bl              # check if at end of list
        je      .L100                # branch #2
        addq    $8, %rsp
        ret
.L100:
        movq    8(%rbx), %rdi        # load tail element of list
        movq    (%rbx), %rbx         # load head element of list
        leaq    -1(%rbx,%rax), %rax  # add it to accumulator
        movq    %rdi, %rbx           # move tail element for next iteration
        jmp     .L101
.L102:
        call    caml_call_gc@PLT
.L104:
        jmp     .L103

I've tried to think like a CPU in order to explain the numbers according to the perf results, but as so many pieces are involved I assumed it would be hard for everything to be correct. Instead, we'll try to get a good intuition by thinking in terms of data dependency. Basically, the assumption is that things that do not depend on each other can be ran in parallel. The second assumption is that thanks to the branch predictor, branch instructions are supposed to have zero cost and they don't introduce data dependencies. Instead, the CPU predicts whether the program will go through the branch and continue execution. In case of misprediction, the CPU will roll back computations for us.

So here is the data dependency chart for this program, showing how two iterations are expected to be ran, with the critical path in red:

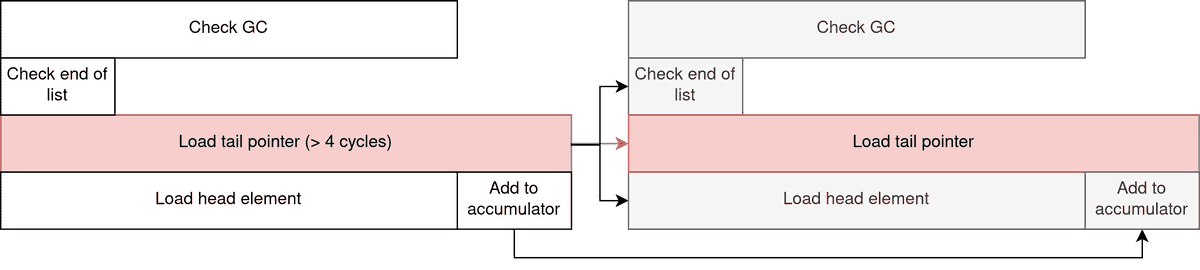
Even if the tail pointer is loaded from cache, we still have to pay a 4 cycles cost to fetch from the L1 cache.

The Check GC part of the loop is independent from the rest, and is useful in a multicore context as every domain of the program has to synchronize when performing garbage collection.

# Value speculation

It's time to open the rune book and perform some dark magic. We know that we won't get past that 4 cycles per iteration bottleneck unless there is a way to bypass the pointer chasing. To do that, we're going to do what was done in the value speculation article, but in pure OCaml.

The principle is the same: cell is converted to a "pointer" using the forbidden Obj.magic function. Using the value of the previous list cell pointer, we can compute delta, the number of bytes between the two last cells. This is used to estimate where will be the next cell. If the prediction is correct, the memory load of the next cell address is effectively bypassed, and the CPU can directly start working on the next iteration. If not, the branch predictor rolls back the computation.

let current : int = Obj.magic cell in                   (* convert list cell to pointer (integer value) *)
let delta : int = current - previous                    (* compute delta with previous pointer *)
let prediction : int list = Obj.magic (current + delta) (* use delta to predict next pointer*)

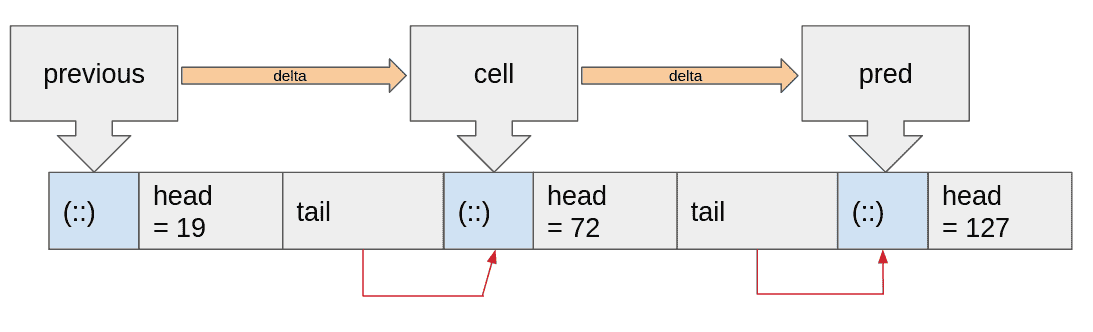
Here is the full program. Note that the delta calculation was inlined for performance reasons.

(current + delta = current + (current - previous) = 2 * current - previous)

let rec seum (previous : int) (accu : int) (cell : int list) =
  match cell with
  | [] -> accu
  | head::tail ->
    let current : int = Obj.magic cell in
    let prediction : int list = (* compute prediction *)
      Obj.magic (2 * current - previous)
    in
    seum
      current
      (accu + head)
      (if prediction == tail then prediction else tail) (* validate prediction *)

The program is executed with the same input and...

 Performance counter stats for './a.out seum':

            944,67 msec task-clock:u                     #    1,000 CPUs utilized
     3 422 107 884      cycles:u                         #    3,623 GHz
    16 006 647 403      instructions:u                   #    4,68  insn per cycle
     5 001 230 197      branches:u                       #    5,294 G/sec
           225 781      branch-misses:u                  #    0,00% of all branches

Per iteration:

• 0.94 nanoseconds
• 3.4 cycles
• 16 instructions
• 5 branches

We got past the bottleneck ! What we're effectively doing is transforming the list iteration into an array iteration. And this works, because there are situations where OCaml lists are allocated in a linear fashion, making the cell addresses predictible. Note in particular the huge number of instructions per cycle.

If you are not convinced, here is an updated dependency diagram for this program.

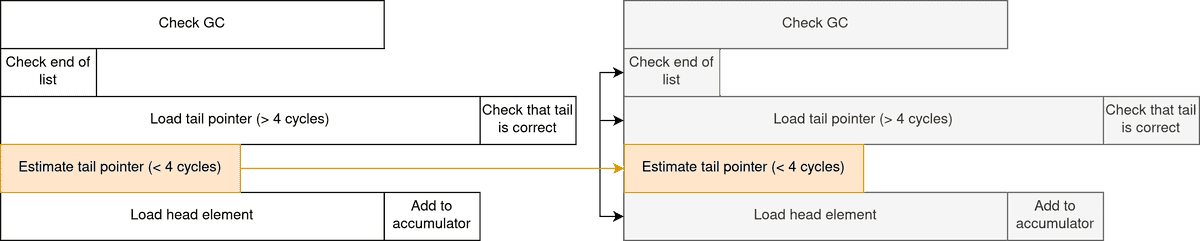
By moving the tail pointer load outside of the critical path, the CPU is able to do more things at once. The following chart shows how one can expect the CPU to execute instructions for three iterations in parallel.

# The crux of the hack

The astute reader will wonder how is it possible to use Obj.magic to transmute the int list to an int. Indeed these OCaml types have different representations.

• An int list is a pointer to an OCaml block allocated on the heap. Due to alignment, it always end with a zero bit.
• An int is a primitive OCaml value, the value n being represented as the tagged integer 2 * n + 1.

This means that usual operations on int values won't work on raw pointers. For example, the addition is implemented as Int.add a b = a + b - 1. The consequence is that adding two raw numbers together using the OCaml addition will subtract one from the result to account for the expected tags.

For subtraction, it is similar: Int.sub a b = a - b + 1.

The magic happens when we're combining an addition and a subtraction, so that the whole operation is correct on both pointers and integers:

Int.add current (Int.sub current previous)
  = current + (current - previous + 1) - 1
  = current + (current - previous)

camlExample__seum_268:
        subq    $8, %rsp
.L103:
        movq    %rax, %rsi
        movq    %rdi, %rax
        cmpq    (%r14), %r15           # check if GC is waiting for us
        jbe     .L104                  # branch #1
.L105:
        testb   $1, %al                # check if at end of list
        je      .L102                  # branch #2
        movq    %rbx, %rax
        addq    $8, %rsp
        ret
.L102:
        movq    8(%rax), %rdx          # load tail element of list cell
        movq    %rax, %rdi             # move cell pointer to %rdi
        salq    $1, %rdi               # multiply pointer by two
        subq    %rsi, %rdi             # subtract previous cell pointer to obtain the prediction
        cmpq    %rdx, %rdi             # compare tail element with prediction
        jne     .L101
        jmp     .L100
.L101:
        movq    %rdx, %rdi             # prediction is incorrect, move the tail element in %rdi
.L100:
        movq    (%rax), %rsi           # load head element of list cell
        leaq    -1(%rbx,%rsi), %rbx    # add to accumulator
        jmp     .L103                  # loop
.L104:
        call    caml_call_gc@PLT
.L106:
        jmp     .L105

# Optimized

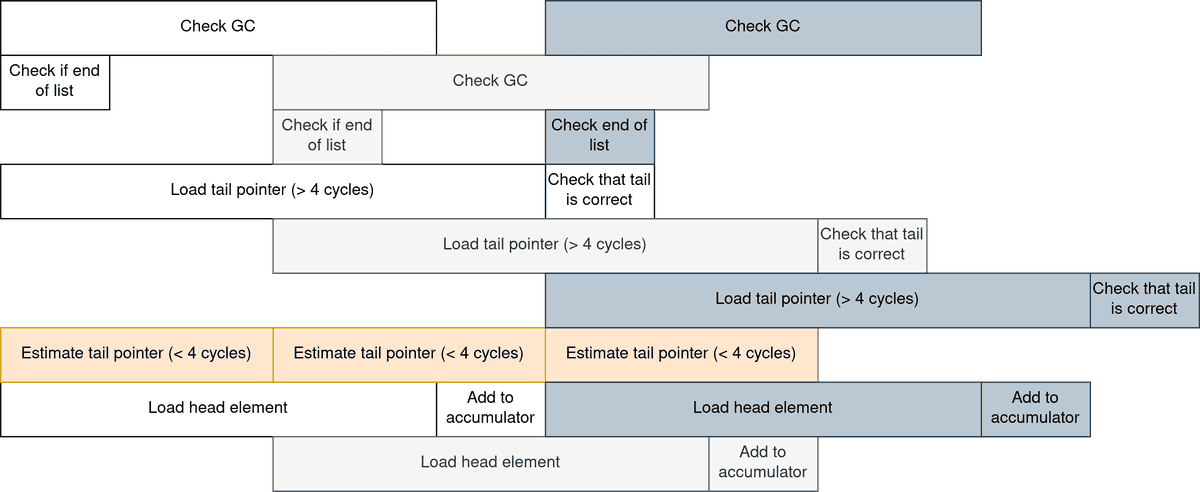
I was not satisfied by this mere 45% improvement. What if the loop was unrolled, so that the CPU has more freedom to move instructions around ?

let rec seum_unroll (previous : int) (accu : int) (cell : int list) =
  match cell with
  | [] -> accu
  | [a] ->  accu + a
  | [a; b] -> accu + a + b
  | [a; b; c] -> accu + a + b + c
  | a::b::c::d::tail ->
      let current = Obj.magic cell in
      let prediction : int list =
        Obj.magic (2 * current - previous)
      in
      seum_unroll
        current
        (accu + a + b + c + d)
        (if prediction == tail then prediction else tail)

The idea is to iterate on the list by chunks of 4 items. There is still the same amount of work to do, but the value prediction trick is performed once every 4 element.

 Performance counter stats for './a.out seum_unroll':

            715,58 msec task-clock:u                     #    0,999 CPUs utilized
     2 410 830 333      cycles:u                         #    3,369 GHz
     7 756 543 257      instructions:u                   #    3,22  insn per cycle
     2 001 229 820      branches:u                       #    2,797 G/sec
           112 956      branch-misses:u                  #    0,01% of all branches

Per iteration:

• 0.72 nanoseconds
• 2.4 cycles
• 7.7 instructions
• 2 branches

91.3% faster. Nice.

According the original article, we're now faster than the naive C implementation, but 2x slower than the hand-optimized one. This is all very synthetic but I found it quite interesting that OCaml is able to benefit from the same hacks as C. Of course this won't be useful in a lot of situations, but maybe one will gain some insights on how modern CPU are able to make programs go fast.

If you like this article I'd be glad to have your feedback. Public discussion on Twitter, Hacker News.